In response to some questions about whether the Lunokhod 2 rover is parked at an azimuth that would allow lunar laser ranging to be successful, LLR data can resolve the question.
First, generally speaking, at least four independent LLR stations have received unambiguous returns from Lunokhod 2, beginning in the early 1970's. The coordinates of the reflector are fit to the data, resulting in a consistent position at the few-centimeter level over decades of ranging. The claim that LLR is being fooled by reflection from terrain must clearly be wrong given the consistent nature of coordinates for the reflector. This is all we really need to be sure that a bona-fide retroreflector (centimeter scale) exists at the location of Lunokhod 2.
We can use the fact that we do see a return from Lunokhod 2 to put
a crude constraint on the rover's azimuth. Nominally, Lunokhod 2
would face selenographic SW, to point toward the center of the face of the
moon. This puts the azimuth at 234 deg; east from north.
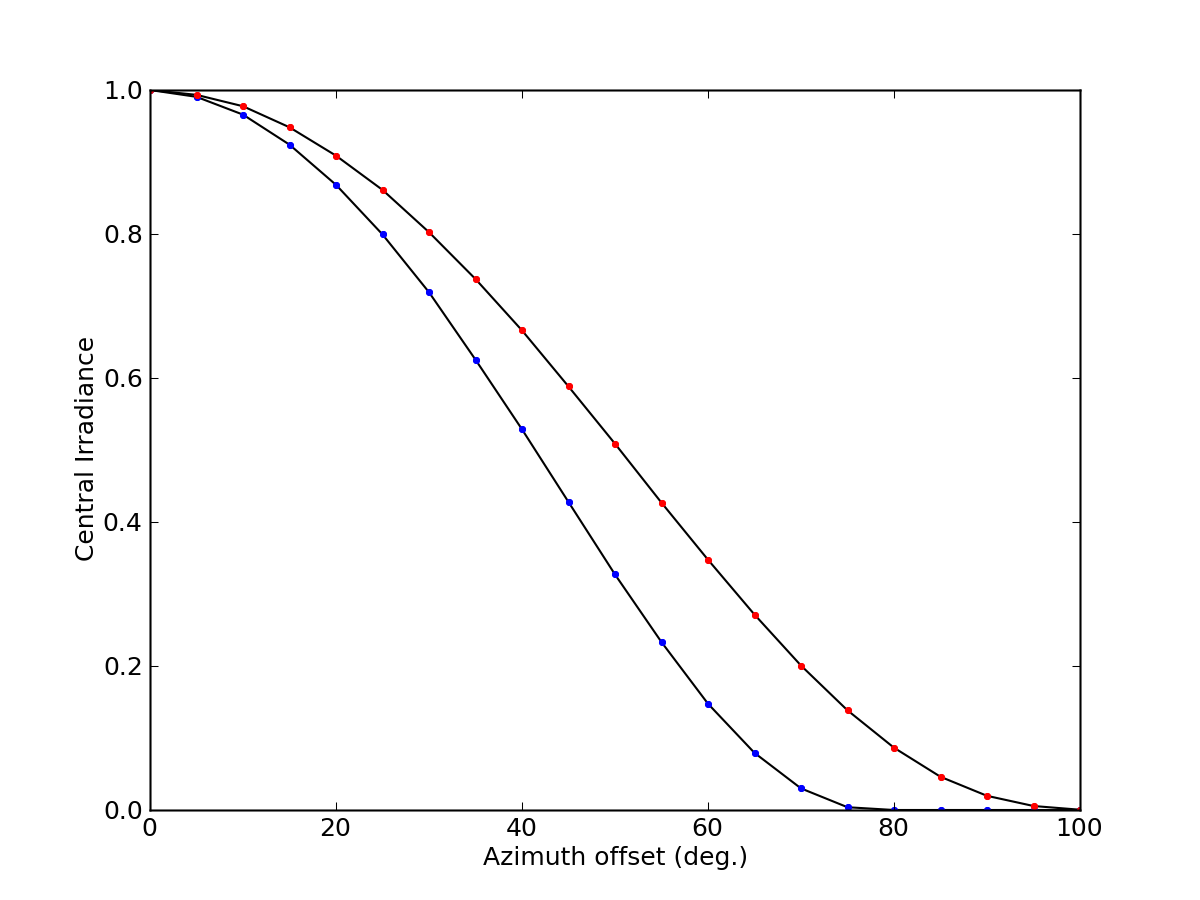
There are limits to how far one can swing the azimuth before the
reflectors stop returning light. Below is a plot for both Lunokhod
reflectors (L1 in blue, L2 in red), showing how much azimuth offset can be
tolerated (in either direction) before the signal is lost. For
Lunokhod 2, the signal is lost once the azimuth offset is more than
about 90°. This means that Lunokhod 2 faces an azimuth between
144°—324°.

But we can go further using timing from APOLLO. Put simply, the temporal signature of the return is compact: on the scale of 0.5 ns wide. At the position of Lunokhod 2, rotating the rover about the vertical axis (i.e., turning it's parking azimuth) would result in a maximum width of about 1.3 ns, when the rover is 90 degrees from the nominal azimuth. Beyond this azimuth, the signal is lost due to the limited angular cross section of the corner cube prisms.
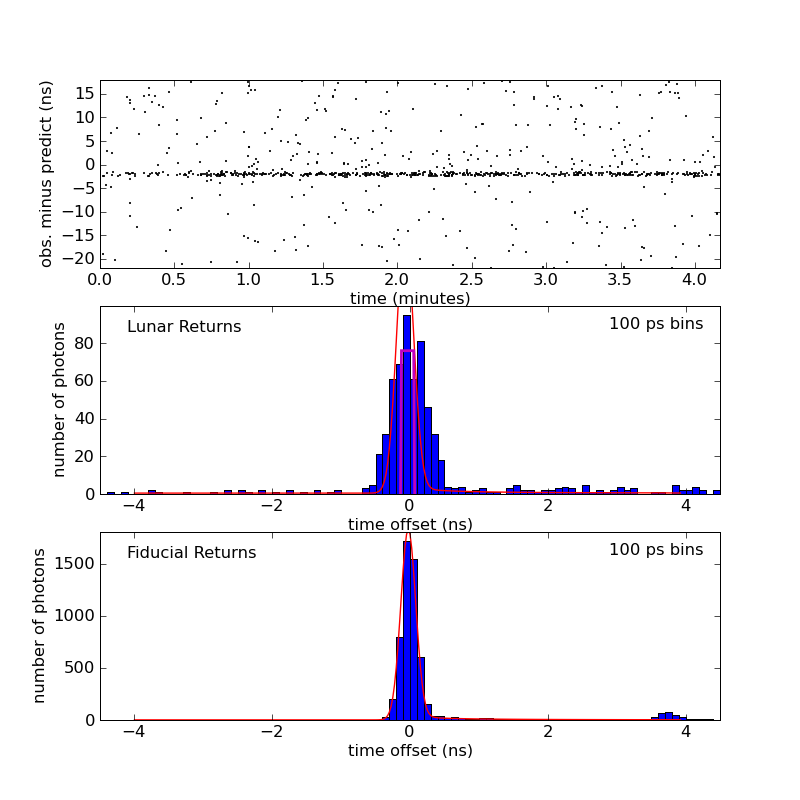
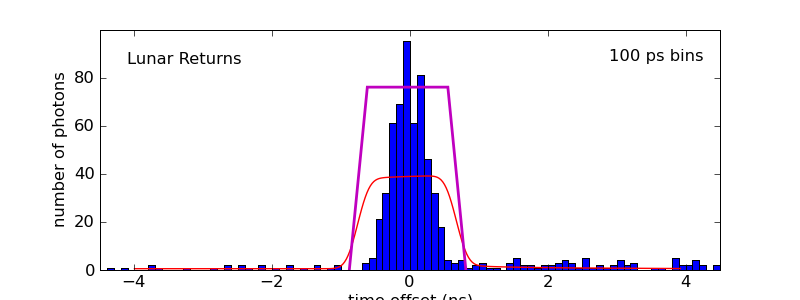
Below is an example (strong) run from Lunokhod 2 (from 2008-08-22).
The upper panel is a segment of the 100 ns range window, showing
scattered background (and dark current) detections, as well as a thin
return from the reflector (terrain could never make a return so strong and
tight!). The middle panel is a histogram of the upper panel. The lower
panel is the system response to the local (fiducial) corner cube, capturing
the laser pulse width, and timing jitter from the detector and electronics.
The only difference between the fiducial return and lunar return is the
finite size of the physical reflector array. The more tilted the array,
the fatter the lunar histogram will be.
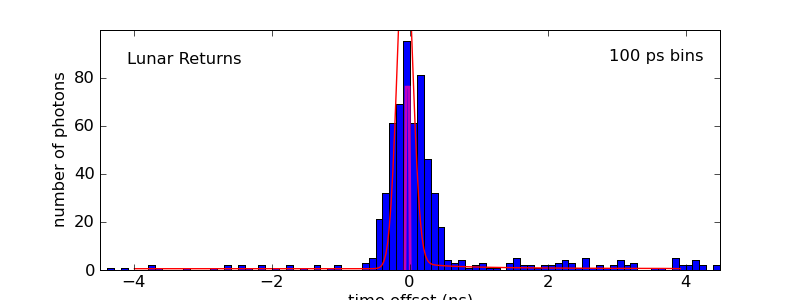
A functional form is fit to the fiducial response, and this function is then convolved with a trapezoid function representing the tilted array. The trapezoid is depicted in the middle panel in magenta, and the convolved function is displayed in red (constrained to match the total photon number). In this case, the nominal (perfect) azimuth is assumed, and the functional form appears to be too narrow for the actual response.
It is not unusual for other influences to broaden the lunar return signal (other sources of jitter not captured by the fiducial), but it would be very odd if the real profile appeared to be narrower than the theoretical curve. All the same, let's reject this nominal fit as being too narrow.
We can broaden the trapezoid in the middle panel by applying an azimuth offset to the reflector. As an aside, the trapezoid is the appropriate shape for a square or rectangular array. This works perfectly well for Apollo reflectors, and is a very good approximation of the Lunokhod array (two rows of 7 reflectors each), but not perfect. In any case, it is certainly good enough to illustrate the point, as the general width is well-represented by the function at hand.
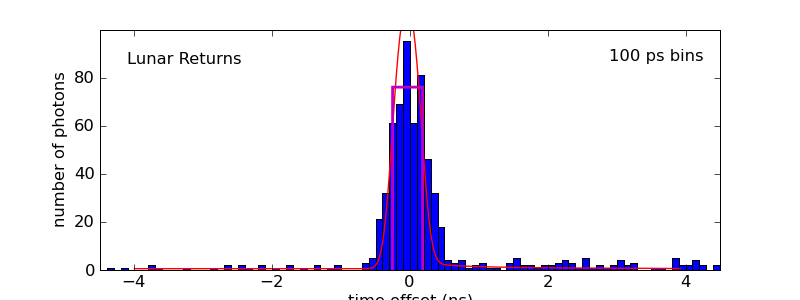
So let's move 10° in either direction. First negative (more toward the south).
Rotating the rover by −10° makes the trapezoid even narrower (at the libration on this particular night), so this is an even worse fit. Let's do +10°, so that the rover faces more toward the selenographic prime meridian:
Better. We actually get the best fit (chi-squared) at +20°:
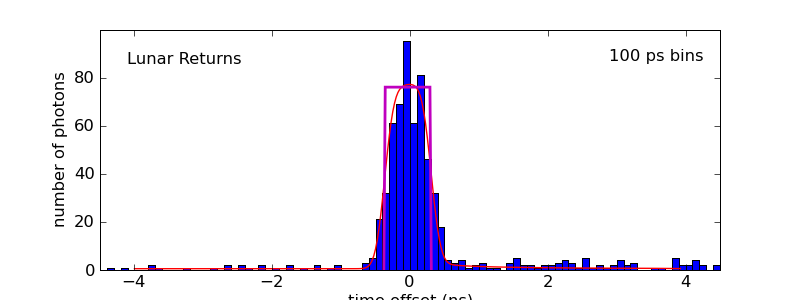
To the eye, this trapezoid is already perhaps a little too wide. When we double this, to +40°—facing nearly due west (274° azimuth), we're clearly out of bounds, and we can confidently say that Lunokhod 2 must be at least facing to the south side of west.
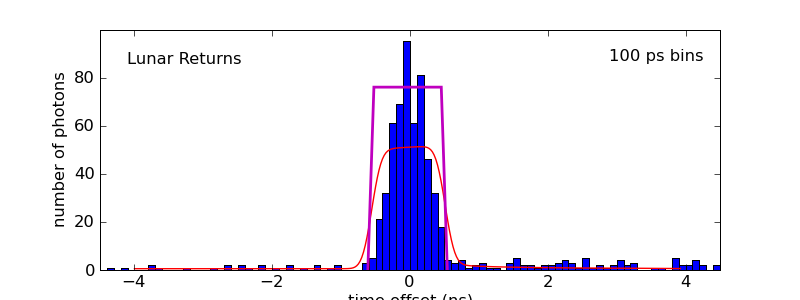
And just for maximal absurdity, let's take it to +90°, now facing NW:
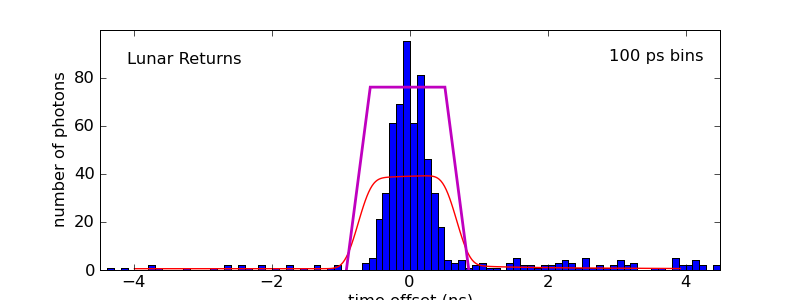
Okay, that was fun. Now let's go farther in the minus direction. At first, the trapezoid got narrower, but it will not continue to do so. It eventually broadens again, and we achieve a minimum chi-squared fit at an azimuth offset of −35°, with the rover facing SSW at 199° azimuth:
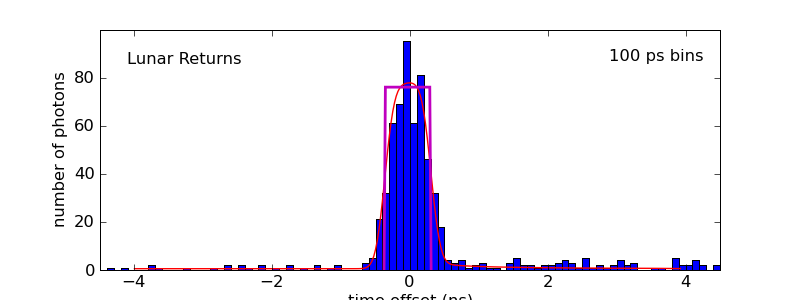
Some LRO images of Lunokhod 2 suggest a southeast orientation, but this is clearly bad news. The most we can go and still expect to see any light return is −90° (144° azimuth), and here's what it looks like:
APOLLO data confines the Lunokhod rover to still point roughly southwest. The reflector is clearly visible, and not hidden from view. A very similar story holds for Lunokhod 1.
One interesting additional connection: having constrained the azimuthal orientation of Lunokhod 2 to be within about 40° of the nominal pointing, we can peg the throughput of the reflector as being at least 65% of the nominal performance. Thus the factor-of-five difference between signal levels from Lunokhod 1 and Lunokhod 2 cannot be attributed to parking. Equally important is the overall factor of ten signal degradation observed in all reflectors. Azimuth orientation of the Lunokhods cannot address this phenomenon (and is utterly unable to explain why the Apollo arrays are similarly afflicted). See this paper (PDF) for background.