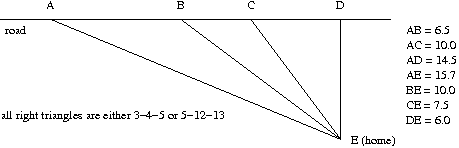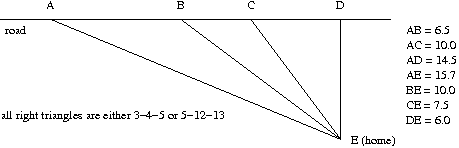Physics 8: Homework 7 Questions
In addition to the problems from the book (14.E.8, 14.E.19, 14.E.20,
14.E.21, 15.E.26), the following problems are a required part of
the homework.
- Get a shiny, bendable thing to explore which kind of curvature produces
"fat" and "skinny" images. Items that work well are CD
cases (with dark background/insert); a cheap, flexible mirror; a large
window pane against a dark (nighttime) background; even a shiny textbook
may do the trick (especially dark and shiny). Now distort the surface to
make your face appear fat or skinny. Which way does the mirror have to
bend to make you look fat: convex (bulging out toward you), or concave (like
looking into a bowl)? Which way makes you look skinny? If you're
ambitious (not required), you may be able to see why by
"raytracing"—drawing the paths of light rays from the sides
of your face, off the mirror (following reflection rules) and to your eye.
The wider the angle your face makes at your eye means the fatter it will
look. Don't exaggerate the curve of the mirror too much or you may get
confusing results—especially in the concave case.
- To convince you that the rules of refraction obey ideas of least-time
propagation paths, consider the analogy of driving speed. Let's say you
can travel at 50 m.p.h. on a straight country road, but your house is 6
miles off the road across a field of dirt. If you can travel only 30
m.p.h. on the dirt, you have to decide where to turn off. Refer to the
diagram below. You could turn off the road at points A, B, C, or D.
Calculate the time it would take to travel the four possible routes to your
home at E given the two different speeds, starting at A. For example,
route ADE takes 0.49 hours. Note which is fastest. The various distances
(in miles) are noted in the diagram). This situation, incidentally, is
equivalent to a refractive index of 1.667 (50/30).
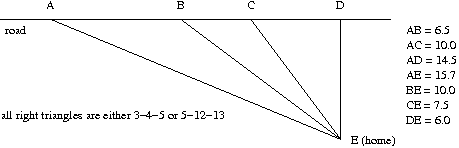
- Now what if you get tires that can handle higher speeds on the dirt,
and you can now go 40 m.p.h. on the dirt (still 50 m.p.h. on the road).
Which path (turnoff) is fastest? You'll need to carry three digits of
precision to distinguish these close numbers. This scenario is equivalent
to a refractive index of 1.25 (50/40).
- Using graphs like the one below, plot the spectrum you would expect to
see from a red light, from a green light, and from a blue light. Draw
three separate graphs for clarity. Don't worry about what happens in the
UV or IR portions: just concentrate on the visible part of the spectrum.
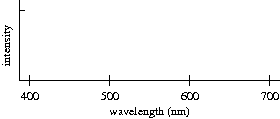
- Using graphs like the one above, draw the spectrum you would expect
to see from a green laser. On the same graph, also draw the spectrum you
would expect to see from a red laser. Be sure to mark which is which.
- Using graphs like the one above, draw the spectrum you would expect to
see from cyan, magenta, and yellow paints (the primary subtractive colors,
absorbing red, green, and blue, respectively). Draw three separate graphs
for clarity.
- Let's say that a particular piece of blue paper absorbs all
red light incident on it (in addition to some green). What color will this
paper look like in a room that is lit up only by a red light?
- If you mix cyan, magenta, and yellow paint together, what color is
likely to result? Keep in mind that these are the primary subtractive
colors—each responsible for absorbing red, green, and blue,
respectively. It may help to consult your spectra from above to confirm
this expectation.
- Red paint must absorb both blue and green light. What two paint colors
(out of the three primary subtractive colors: cyan, magenta, yellow)
would you mix together to get red, then?